LIMITES

                             

Cálculo de límites

Más de 50 límites resueltos y explicados

En esta página calculamos límites de funciones de una variable. Primero, hacemos una pequeña introducción y recordamos los conceptos de límite, límites laterales e indeterminaciones. Después, proporcionamos algunas reglas y procedimientos útiles para calcular límites y evitar las indeterminaciones.

En total, resolvemos detalladamente más de 50 límites, sin utilizar la regla de L'Hôpital ni infinitésimos.

Índice:

1. Introducción
2. Concepto de límite
3. Definición formal
4. Límites laterales
5. Límites infinitos
6. Reglas básicas
7. Primeros límites resueltos (básicos)
8. Indeterminaciones
9. Procedimientos o técnicas
10. Más límites resueltos

Más límites resueltos:

• 50 límites resueltos
• Indeterminación 0/0
• Indeterminación ∞/∞
• Indeterminación 0·∞
• Indeterminación 1^∞

1. Introducción

Las funciones matemáticas se utilizan en otros ámbitos, por ejemplo, para calcular los beneficios o los costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función.

Por ejemplo, la siguiente función no está definida en $x=0$ ni en $x=-1$ (porque no se puede dividir entre $0$):

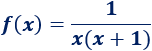
Sin embargo, sí podemos preguntarnos cómo se comporta la función cuando $x$ se aproxima a $0$ o cuando se aproxima a $-1$.  ¿Y si $x$ crece o decrece indefinidamente? Los límites de la función $f$ nos proporcionan las respuestas.

Además de ayudarnos a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.

2. Concepto de límite

Dada una función $f:R\to R$ y un punto $x_0\in R$, el límite de $f$ cuando $x$ tiende a $x_0$ se representa como

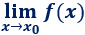
En un principio, este límite es el valor que toma $f$ en el punto $x_0$, es decir, $f\left(x_0\right)$. Si $f\left(x_0\right)$ no existe (por ejemplo, cuando $x_0$ anula el denominador de $f$), entonces el límite es el valor al que $f$ se aproxima cuando $x$ se aproxima a $x_0$.

Por ejemplo, sea la función

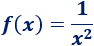
No existe $f\left(0\right)$, pero cuanto más se aproxima $x$ a $0$, la función crece más y más, como podemos observar en la gráfica:

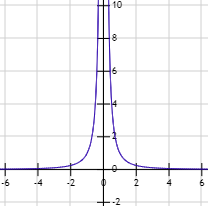
Por tanto, el límite de $f$ cuando $x$ tiende a $0$ es infinito:

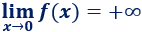
También, podemos predecir el comportamiento de la función cuando $x$ crece o decrece indefinidamente (cuando $x$ tiende a $\pm \infty$). Cuando esto ocurre, la función $f\left(x\right)=1/x^2$ se aproxima cada vez más a $0$:

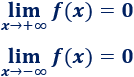
3. Definición formal

Ver texto

4. Límites laterales

Ver texto

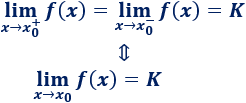
5. Límites infinitos

Hemos estado hablando, básicamente, de límites en puntos finitos $x_0\in R$, pero también podemos preguntarnos cuál es límite de una función cuando $x$ crece o decrece indefinidamente, es decir, cuando $x\to +\infty$ y cuando $x\to -\infty$.

Ver ejemplo

Obviamente, no podemos hablar de límites laterales cuando $x$ tiende a infinito.

6. Reglas básicas

Hasta el momento, no hemos explicado cómo calcular los límites.

1. Lo primero que hacemos para calcular el límite de $f$ en el punto $x_0$ es comprobar si se puede calcular $f\left(x_0\right)$ porque, en este caso, el límite es dicho valor:

   

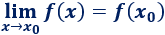
   Es decir, en este caso sólo hay que cambiar las $x$ por $x_0$.

   Ver ejemplo

   Nota: en una función definida a trozos, hay que calcular primero los límites laterales en $x_0$ si es un punto de cambio de definición.

2. Es importante comprobar que la función está escrita en su mínima expresión.

   Ver ejemplo

Ahora vamos a ver las reglas que nos permiten calcular los límites cuando sustituimos $x$ por $x_0$. Escribiremos el signo de interrogación "?" para las indeterminaciones, de las cuales hablaremos más adelante.

Sea $K$ un número real distinto de $0$.

Sumar o restar infinito:

La resta de infinitos de signo distinto es indeterminado: $\infty -\infty =?$.

Multiplicar por infinito:

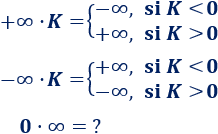
El producto $0\cdot \infty$ es una indeterminación.

El producto de infinitos es infinito. El signo se obtiene por la regla de los signos:

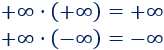
Dividir entre cero:

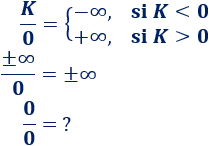
El cociente $0/0$ es una indeterminación.

Dividir entre infinito:

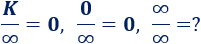
El cociente $\infty /\infty$ es una indeterminación.

Elevar a $0$:

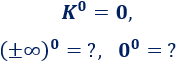
Las potencias ${\infty }^0$ y $0^0$ son indeterminaciones.

Elevar a infinito:

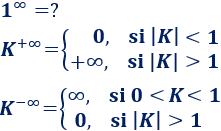
La potencia $1^{\infty }$ es una indeterminación.

Nota: $0^{\infty }=0$ y ${\infty }^{\infty }=\infty$ no son indeterminaciones.

7. Primeros límites resueltos (básicos)

Límite 1

Solución

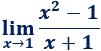
Límite 2

Solución

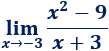
Límite 3

Solución

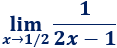
Límite 4

Solución

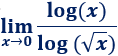
Límite 5

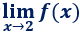
siendo $f$ la siguiente función definida por partes:

Solución

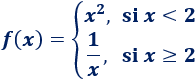
8. Indeterminaciones

Las indeterminaciones son las 7 operaciones algebraicas siguientes cuyo resultado no podemos predecir:

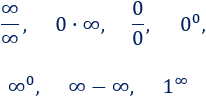
Por ejemplo, en los dos siguientes límites aparece la indeterminación cociente de infinitos:

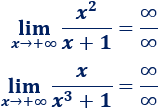
El resultado del primer límites es $+\infty$ y el del segundo es $0$.

En el siguiente apartado vemos algunos procedimientos para resolver las indeterminaciones.

9. Procedimientos o técnicas

La mayoría de los procedimientos los utilizamos cuando $x\to \infty$.

Cociente de polinomios:

En el límite de un cociente de polinomios $P\left(x\right)/Q\left(x\right)$ suele aparecer un cociente de infinitos ($\infty /\infty$). Escribimos $\delta P$ y $\delta Q$ para referirnos al grado del polinomio $P$ y $Q$, respectivamente:

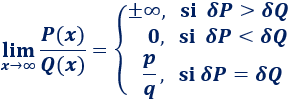
En el primer caso, el signo del infinito depende de los grados de los polinomios y de sus coeficientes.

En el tercer caso, $p$ es el coeficiente director de $P\left(x\right)$ y $q$ es el de $Q\left(x\right)$.

Problema 1

Calcular los siguientes límites:

• ${lim}_{x\to +\infty }\frac{x^3}{x^2+1}$

• ${lim}_{x\to -\infty }\frac{x^3}{x^2+1}$

• ${lim}_{x\to -\infty }\frac{-x^3}{x^2+1}$

• ${lim}_{x\to +\infty }\frac{x^3}{1-x^2}$

Solución

Cociente de exponenciales:

Normalmente, para resolver límites con exponenciales, dividimos la función entre alguna de las exponenciales (generalmente, la que tiene base mayor para conseguir bases menores que 1).

Problema 2

Calcular los siguientes límites:

• ${lim}_{x\to -\infty }\frac{3^x}{2^x-5}$

• ${lim}_{x\to -\infty }{3}^x\cdot x-2^x$

• ${lim}_{x\to +\infty }\frac{ln\left(3^x\right)}{x-2}$

• ${lim}_{x\to +\infty }\frac{ln(5^x+3^x+2^x)}{ln(5^x+2^x)}$

Solución

Indeterminación $1^{\infty }$:

Esta indeterminación aparece, normalmente, en los límites con la forma

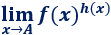
donde la función $f\left(x\right)$ tiende a 1 y $h\left(x\right)$ tiende a infinito. El punto $A$ del límite puede ser un punto finito o $\pm \infty$.

En este caso, aplicamos la siguiente fórmula:

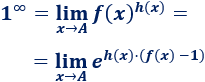
Problema 3

Calcular los siguientes límites:

• ${lim}_{x\to +\infty }{\left(\frac{1+x}{x-1}\right)}^x$

• ${lim}_{x\to +\infty }{\left(1+\frac{1}{x}\right)}^x$

• ${lim}_{x\to +\infty }{\left(1+\frac{1}{x^3}\right)}^{x^2}$

• ${lim}_{x\to +\infty }{\left(1+\frac{x}{1+2x^2}\right)}^x$

Solución

Cociente de raíces:

Cuando la función está formada por un cociente en el que aparecen raíces, el límite depende del orden de las raíces, al igual que en los cocientes de polinomios.

Suelen aparecer las indeterminaciones resta de infinitos y cociente de infinitos. Normalmente, es suficiente multiplicar y dividir por el conjugado y/o comparar los órdenes de las raíces y grados de las $x$.

Fórmulas que pueden ayudar (para resta de infinitos):

Ver ejemplo

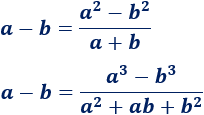
Problema 4

Calcular los siguientes límites:

• ${lim}_{x\to +\infty }\frac{3x}{\sqrt{x+3x^2}}$

• ${lim}_{x\to +\infty }\frac{\sqrt[3]{32x-1}-\sqrt{2x^2+1}}{\sqrt[3]{35x^3-2}}$

• ${lim}_{x\to +\infty }\sqrt{x^2+x-1}-\sqrt{x^2-2x}$

• ${lim}_{x\to +\infty }\frac{\sqrt{3x^2-2x}-\sqrt{3x^3+5x^2}}{\sqrt{5x}}$

Solución

Comparación de funciones:

Muchas veces, es fácil calcular el límite de una función simplemente comparando las funciones que conforman la propia función.

Por ejemplo, el límite cuando $x$ tiende a $+\infty$ de la función $x^5-x^2$ es $\infty -\infty$. Sin embargo, como $x^5$ crece más rápido que la función $x^2$, el límite es $+\infty$. Dicho de otra forma, el orden del infinito del límite de la primera función es mayor que el de la segunda, así que el resultado es $\infty$.

Otros ejemplos:

• un monomio crece más rápido que un logaritmo,

• un monomio crece más rápido que una raíz,

• una exponencial crece más rápido que un monomio.

Problema 5

Calcular los siguientes límites:

• ${lim}_{x\to +\infty }\frac{x}{e^x}$

• ${lim}_{x\to +\infty }\frac{x-ln\left(x\right)}{x}$

• ${lim}_{x\to +\infty }x\cdot ln\left(x\right)-x\cdot e^x$

• ${lim}_{x\to +\infty }\frac{2^x+x^2}{3^x}$

Solución

Aplicación de logaritmos:

Las propiedades de los logaritmos pueden ser útiles para calcular límites, sobre todo, cuando aparecen exponentes. Para ello, utilizamos la propia definición del logaritmo:

De este modo,

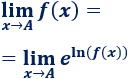
Problema 6

Calcular los siguientes límites:

• ${lim}_{x\to +\infty }{x}^{\frac{1}{x}}$

• ${lim}_{x\to +\infty }{\frac{1}{x}}^{\frac{1}{x}}$

• ${lim}_{x\to +\infty }\sqrt[3x^2]{3x^2\frac{e^{x^2}}{x^5}}$

• ${lim}_{x\to +\infty }\frac{1}{x^2}\cdot x^{\frac{1}{x^2+1}}$

Solución

10. Más límites resueltos

Límite 6

Solución

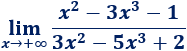
Límite 7

Solución

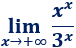
Límite 8

Solución

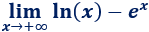
Límite 9

Solución

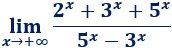
Límite 10

Solución

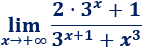
Límite 11

Solución

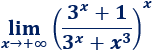
Límite 12

Solución

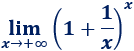
Límite 13

Solución

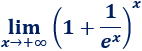
Límite 14

Solución

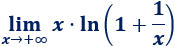
Límite 15

Solución

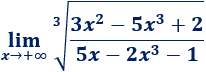
Límite 16

Solución

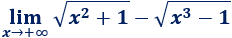
Límite 17

Solución

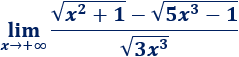
Límite 18

Solución

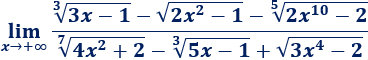
Límite 19

Solución

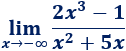
Límite 20

Solución

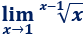
Límite 21

Solución

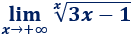
Límite 22

Solución

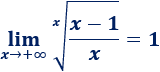
Límite 23 (difícil)

Solución

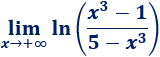
Límite 24

Solución

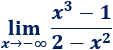
Límite 25

Solución

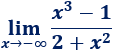
Límite 26

Solución

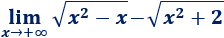
Límite 27

Solución

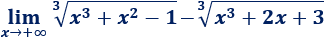
Límite 28

Solución

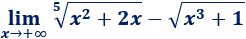
Límite 29

Solución

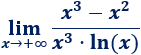
Límite 30

Solución

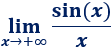
Límite 31

Solución

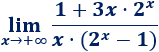
Límite 32

Solución

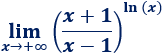
Límite 33

Solución

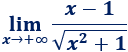
Límite 34

Solución

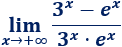
Límite 35

Solución

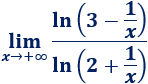
Límite 36

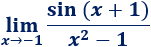
Ayuda: utilizad el siguiente límite:

Solución

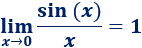
Límite 37

Ayuda: utilizad el siguiente límite:

Solución

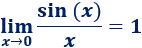
Límite 38

Solución

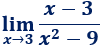
Límite 39

Solución

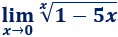
Límite 40

Solución

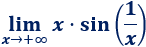
Límite 41

Demostrar el límite siguiente, que se ha empleado en varias ocasiones en esta página:

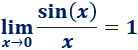
Ayuda: representación del coseno de $x$, del arco de circunferencia con ángulo $x$ y de la tangente de $x$ en un circuncerencia de radio $R=1$, siendo $0<x<\pi /2$:

Solución

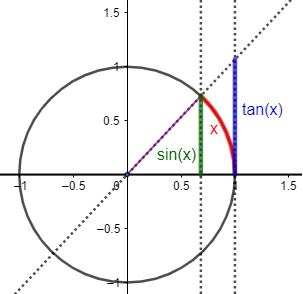
Límite 42

Solución

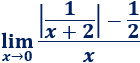
Límite 43

Solución

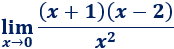
Límite 44

Solución

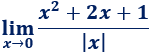
Límite 45

Solución

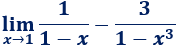
Límite 46

Solución

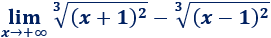
Límite 47

Solución

Límite 48

Solución

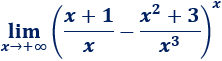
Límite 49

Comprobar la fórmula que empleamos para la indeterminación uno elevado a infinito ($1^{\infty }$):

Solución

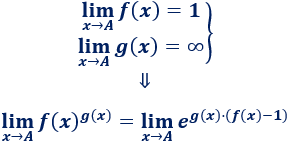
Límite 50

Solución

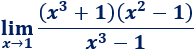
Más límites resueltos:

• Cálculo de límites
• La regla de L'Hôpital
• Límites de sucesiones